Solving 2 X^x^x^x: Your Guide To Taming Tricky Exponential Equations
Have you ever looked at a math problem and thought, "What on earth is that?" Well, the equation 2 x^x^x^x is that kind of problem. It looks really wild, almost like a tower of numbers and variables reaching for the sky. For many, just seeing it can make you feel a little lost, perhaps even a bit curious about how anyone could possibly figure it out. It's a classic example of how math can sometimes throw you a curveball, presenting something that seems incredibly complex at first glance.
This particular problem, 2 x^x^x^x, is a wonderful example of what we call iterated exponentiation. It means you're taking 'x' to the power of 'x', then taking that result to the power of 'x' again, and so on, for a total of four times. Then, the whole thing equals two. It's a bit like a mathematical riddle, and finding the value of 'x' that makes this true is quite a challenge for traditional methods, you know, the kind you might learn in a typical classroom.
Luckily, you don't have to face such a puzzle all by yourself. In our current time, with all the smart tools available, figuring out problems like 2 x^x^x^x has become much more approachable. We're going to explore what makes this equation so interesting and, more importantly, how you can actually go about solving it, perhaps even with some clever help from online math solvers. So, let's get into it, shall we?
Table of Contents
- What Does x^x^x^x = 2 Even Mean?
- Why Solving This Equation Is a Real Brain-Teaser
- Finding the Solution: The Modern Approach
- Exploring Related Math Concepts
- Frequently Asked Questions About Tricky Equations
- Ready to Tackle More Math Puzzles?
What Does x^x^x^x = 2 Even Mean?
When you see something like x^x^x^x, it's not just a typo or a random string of characters. This is a very specific type of mathematical expression. It's a tower of exponents, where each exponent is the variable 'x' itself. So, to break it down, it means x raised to the power of (x raised to the power of (x raised to the power of x)). That's a lot of 'x's stacked up, you know? It's often called tetration or iterated exponentiation, and it gets tricky because the base and the exponent are the same, and it keeps repeating.
For our problem, 2 x^x^x^x, it's actually written a little differently. It means x to the power of (x to the power of (x to the power of x)), and that entire result is equal to 2. This structure is what makes it so different from a simple equation like x^2 = 4, where you can easily find x. Here, the variable is nested deep inside the exponential structure, which makes it a fun challenge for anyone who likes to play with numbers, or even for someone just trying to understand more about how these kinds of equations work.
As of June 10, 2024, these kinds of problems continue to fascinate math enthusiasts and computer scientists alike. They often appear in areas of mathematics that explore beyond basic algebra, pushing the boundaries of what we can solve directly. So, understanding what this means is the very first step in trying to find a way to solve it, and it really sets the stage for the interesting methods we might use.
- Emily Compagno Husband
- Brigitte Macron As A Child
- Is David Bromstad Married
- Omni Calculator
- Bradley Cadenhead
Why Solving This Equation Is a Real Brain-Teaser
Solving an equation like x^x^x^x = 2 isn't like solving a typical linear or quadratic equation. Those usually have straightforward steps, like isolating 'x' or using a specific formula. But with this kind of iterated exponent, things get quite a bit more complicated. There isn't a simple algebraic trick or a neat formula you can just apply to peel back the layers and find 'x'. It's a bit like trying to untie a very, very tangled knot, if you think about it.
The Iterated Exponentiation Hurdle
The main difficulty here comes from the repeated exponentiation. When you have x^x, it's already a function that grows incredibly fast. Now, imagine x^x^x, and then x^x^x^x. Each new layer of 'x' as an exponent makes the function behave in ways that are very hard to predict or manipulate with standard algebraic operations. For instance, you can't just take a logarithm of both sides repeatedly to simplify it, because the 'x' is both the base and part of the exponent, and that makes things quite messy. It's a bit of a mathematical puzzle that requires a different way of thinking, or so it seems.
This kind of structure means that the equation doesn't fit neatly into the categories of problems that have simple, closed-form solutions using elementary functions. You can't just move terms around or factor things out in the usual way. It really asks you to look for other approaches, perhaps something outside the box of what you might typically do in an algebra class. It's a good example of how some math problems need a different kind of tool to be solved, or at least to get a good estimate of the answer.
When Algebra Hits Its Limits
Most of the time, when we solve for 'x', we're using algebraic substitutions, maybe working with exponents, or dealing with linear and polynomial expressions. But with x^x^x^x = 2, standard algebraic methods just don't quite cut it. You can't easily isolate 'x' using addition, subtraction, multiplication, division, or even basic logarithms. The equation just doesn't cooperate in that way, you know?
This is where we start to see that some equations don't have what mathematicians call an "analytic solution" using only basic functions. Instead, their solutions might involve special functions, like the Lambert W function, which is a bit more advanced and not something you'd typically encounter in introductory math. Or, and this is very important, they might require numerical methods, which means finding an approximate answer through calculations rather than an exact, neat number. So, in a way, it shows us the boundaries of what simple algebra can do.
Finding the Solution: The Modern Approach
Since direct algebraic methods often fall short for equations like x^x^x^x = 2, we turn to more modern approaches. These usually involve using computational tools that can handle the complexity and perform calculations that would be incredibly tedious, or even impossible, to do by hand. It's like using a super-smart assistant to help you with a really tough job, you know?
The Role of Online Math Solvers
Online math solvers have really changed the way people approach difficult equations. They're like having a very knowledgeable tutor available any time, ready to help you with a wide range of math problems. Whether you're dealing with basic arithmetic, complex calculus, or linear algebra, these tools can provide assistance. They are designed to show you the solution, sometimes even with a graph, and, very importantly, they often provide detailed steps and explanations for each part of the problem. This means you don't just get the answer; you also get to learn how to get there, which is pretty neat.
These solvers are especially good for problems where you need to "solve for x." You can just enter your problem, and the calculator will work through the equation to show you the result. They can handle solving in one variable or many, and the equations section lets you tackle a single equation or a whole system of equations. So, if you're looking for an exact answer, they can often find it, or if that's not possible, they can give you a numerical answer with almost any accuracy you might need. It's a powerful way to check your homework problems online, or just to explore mathematical concepts on your own time.
How Symbolab Makes It Simple
When it comes to tackling equations like 2 x^x^x^x, a tool like Symbolab really shines. It's a very helpful step-by-step calculator that can handle a vast array of math problems. You can use it for algebra, calculus, and many other math areas, getting help right on the web or through its math app. For instance, with an equation like ours, you just type it in, and the calculator will walk you through the steps necessary to simplify and solve it. Each step is followed by a brief explanation, which is really useful for learning.
This free equation solver helps you with various types of equations, including linear, quadratic, and polynomial systems. It gives you answers, graphs, roots, and even alternate forms of the solution. It actually solves algebra problems and walks you through them, making it a good learning tool. The equation solver lets you enter your problem and see the result, and it's quite interesting to see how it handles things like exponential expressions and logarithmic expressions, which are key to understanding our problem. You can usually find the exact answer or, if necessary, a numerical answer to almost any accuracy you require, which is pretty amazing.
Beyond just solving, Symbolab offers features like an inequalities section, where you can solve an inequality or a system of inequalities for a single variable, and you can also plot inequalities in two variables. It's an online calculator for solving algebraic equations, and it truly makes it easy to check your homework problems online. You can click on examples to see the algebra solver in action, or read a calculator tutorial to learn more about its capabilities. It's also great for exploring math with its beautiful, free online graphing calculator, where you can graph functions, plot points, visualize algebraic equations, add sliders, and even animate graphs, and more. This visual aspect can be very insightful when dealing with functions that have multiple intersections, or when trying to understand the behavior of complex expressions. It’s a very comprehensive tool for anyone trying to get a handle on different methods to solve for x, gaining insights into exponential functions and how they might intersect with other types of equations, too.
The system lets you solve an equation, an inequality, or a system, making it quite versatile. It's an easy way to check your homework problems online, and it really helps you apply mathematical equations and formulas. You just type in any equation to get the solution, steps, and graph. It's interesting to see that sometimes, two functions can actually have three intersections, and the solver can help visualize that. Also, a non-rational solution can be approximated by an iterative representation, which is a method Symbolab can help demonstrate. So, it covers a lot of ground, from algebraic substitutions to intercepts, and from various expressions to solving inequalities.
Beyond Just the Answer: Steps and Graphs
What makes a tool like Symbolab particularly helpful isn't just that it gives you the answer to x^x^x^x = 2. It's the "how" that matters just as much. Getting detailed steps means you can follow along with the logic, understand each transformation, and see how the problem is broken down into manageable pieces. This is crucial for learning, as it helps you build your own problem-solving skills rather than just relying on a machine for the final number. It's a bit like getting directions to a new place; you want to know the turns, not just the destination, right?
Moreover, the ability to graph functions and visualize algebraic equations is a game-changer. For an equation like x^x^x^x = 2, you might not get a simple, exact answer that's a whole number or a neat fraction. Often, the solution is an irrational number, which means it goes on forever without repeating. By graphing, you can see where the function y = x^x^x^x intersects with the line y = 2. This visual representation can give you a very good idea of the solution's approximate value and even show if there are multiple solutions. It's a powerful way to gain insights into the behavior of these exponential functions and their intersections with linear equations, so it really helps to make sense of things.
Exploring Related Math Concepts
When you tackle an equation like 2 x^x^x^x, you're actually touching on some pretty interesting math concepts that go beyond just finding 'x'. It opens up discussions about how functions behave, how we can approximate answers when exact ones are hard to find, and the different ways we can represent mathematical ideas. It's a good way to see how various parts of math connect, you know?
Functions and Their Intersections
Think about the equation x^x^x^x = 2 as two separate functions: one is y = x^x^x^x, and the other is y = 2. When you solve the equation, you're essentially looking for the point or points where these two functions meet on a graph. These meeting points are called intersections, and the x-values at these points are the solutions to your original equation. It's a very visual way to understand what "solving for x" actually means, particularly for equations that are hard to solve algebraically.
It's quite fascinating to see how complex functions like x^x^x^x behave. Sometimes, you might find that the two functions actually have three intersections, or just one, or even none at all, depending on the specific numbers involved. Graphing tools, as we discussed, are incredibly useful for visualizing these intersections. They help you understand not just the answer, but also the nature of the solution and how the functions interact with each other. This visual insight can really deepen your appreciation for how math works, so it's a very helpful approach.
The Power of Numerical Approximation
For equations where finding an exact, neat answer is very difficult or impossible, mathematicians often turn to numerical approximation. This means finding a value that is very, very close to the actual solution, to almost any accuracy you might need. It's like finding a really good estimate when you can't get the precise measurement. For something like x^x^x^x = 2, the non-rational solution can be approximated by an iterative representation. This involves starting with an educated guess and then repeatedly refining that guess until it gets closer and closer to the true answer. It's a process of getting more and more precise, you know?
This method is widely used in many fields, especially in computer science and engineering, where exact answers might not be practical or even exist. Online solvers are very good at performing these iterative calculations quickly and accurately. They can take an initial estimate and run through many cycles of refinement, giving you a highly accurate numerical answer in seconds. This capability is a testament to the advancements in computational math, allowing us to tackle problems that were once considered too hard to solve. So, even if there isn't a simple number that pops out, we can still get a very good idea of what 'x' is.
Frequently Asked Questions About Tricky Equations
People often have questions when they encounter equations that look a bit unusual or challenging. Here are a few common ones that come up, especially when dealing with exponential expressions like x^x^x^x.
How do you solve x^x = 2?
Solving x^x = 2 is a simpler version of our main problem, but it still shows the difficulties of iterated exponentiation. For this one, a common approach involves recognizing that if x equals the square root of 2 (approximately 1.414), then (square root of 2) raised to the power of (square root of 2) is indeed very close to 2. It's not something you can solve with simple algebra. Often, you'd use a graphing calculator to find the intersection of y = x^x and y = 2, or use numerical methods to get a very close approximation. It’s a good starting point to understand the complexities involved with these kinds of expressions, you know?
What is the solution to x^x^x^x?
For the equation x^x^x^x = 2, the solution for 'x' is not a simple whole number or fraction. It's an irrational number, meaning its decimal representation goes on forever without repeating. To find it, you typically need to use numerical methods or a powerful online calculator. The solution is approximately 1.166. It's a value that, when raised to itself four times in that specific iterated way, results in 2. This shows how some numbers just don't fit neatly into our everyday number system, and we need special tools to find them, or so it seems.
Can all equations like x^x^x... be solved easily?
No, not all equations involving iterated exponentiation can be solved easily, or even at all, using standard algebraic techniques. The difficulty increases significantly with each additional layer of 'x' in the exponent tower. While some simpler cases, like x^x = 2, might have solutions that can be found through observation or basic numerical methods, more complex ones often require specialized functions or advanced computational tools for approximation. So, it's not a straightforward path for every single one, and you really need to pick the right tool for the job.
Ready to Tackle More Math Puzzles?
Figuring out an equation like 2 x^x^x^x might seem like a huge task at first, but as we've seen, with the right approach and the right tools, it becomes a fascinating challenge you can actually work through. It's a good reminder that math isn't always about simple formulas; sometimes it's about exploring new ideas and using clever methods to find answers. The journey of solving these kinds of problems can teach you a lot about the deeper parts of mathematics and how numbers really behave, you know?
Whether you're curious about the exact answer, want to see the step-by-step process, or just want to visualize the functions involved, modern online solvers are there to help. They make complex math much more approachable and help you gain insights into things like algebraic substitutions, exponents, and the behavior of functions. So, why not give it a try yourself? You can explore more about iterated exponentiation on a resource like the Wikipedia page on Tetration, which provides a good overview of this mathematical concept. Learn more about equation solving on our site, and perhaps you'd like to check out our calculator tutorial to get started. It's a great way to expand your math skills and see what else you can solve!
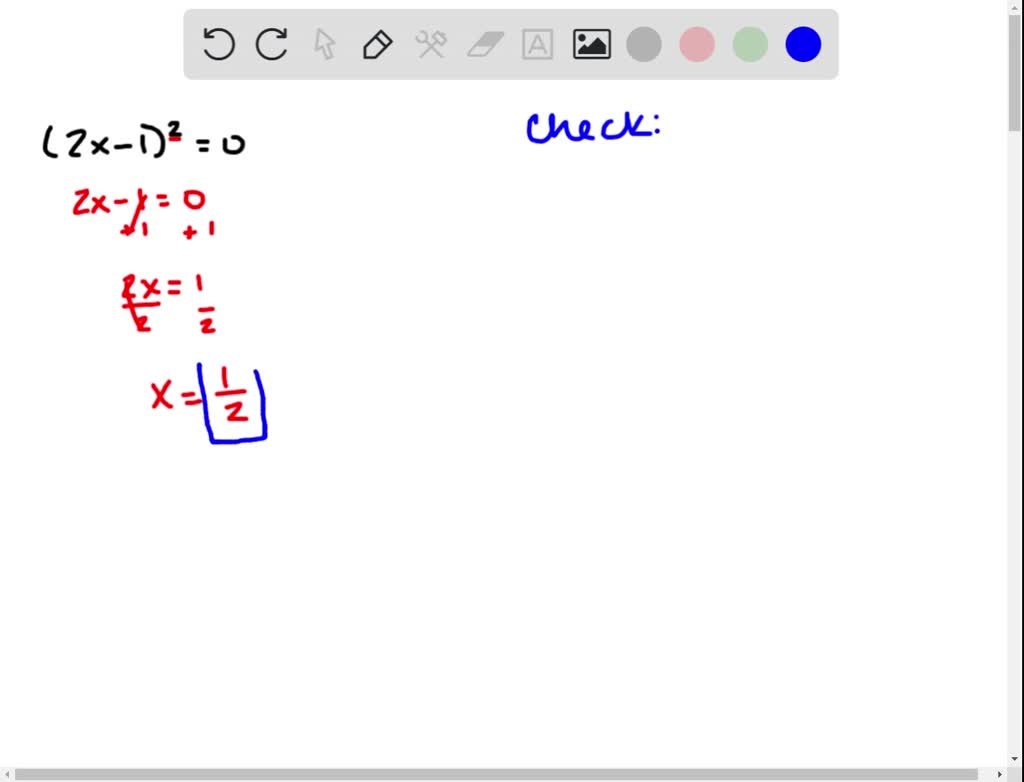
⏩SOLVED:Solve. (2 x-1)^2=0 | Numerade
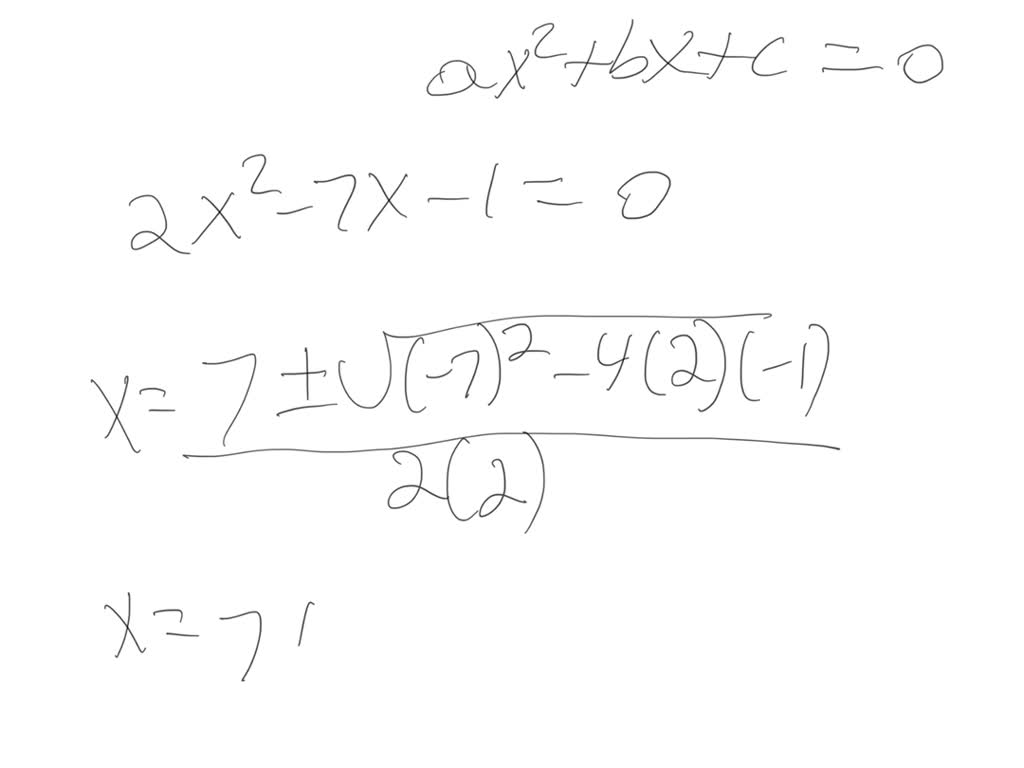
SOLVED:Solve: 2 x^2-7 x-1=0
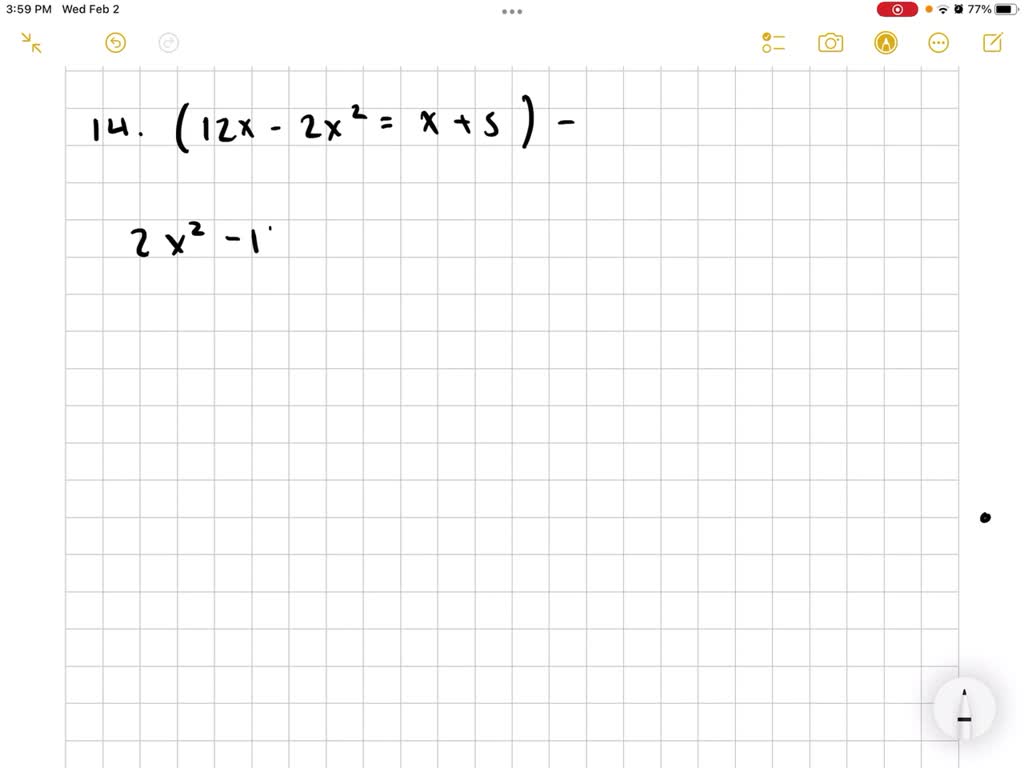
SOLVED:Solve. 2 x x+5=16-x