How To Find Area: Your Simple Guide To Measuring Space
Ever wondered how much paint you need for a wall, or perhaps the amount of carpet for a room? Knowing how to find area is a really useful skill for everyday life. It helps us figure out the size of flat surfaces. Think of it as discovering how much "stuff" can fit onto a flat shape, or how much material you might need to cover it up. This basic idea has so many practical uses, and it's a fundamental concept in geometry, too.
For instance, if you are planning a garden, you need to know the area of the plot to buy the right amount of soil or seeds. Maybe you are considering a new kitchen countertop. That, too, needs an area calculation. It is a way to define the size of a shape, giving us a clear measure of the space it takes up. This understanding is quite important for many tasks, you know, both big and small.
My text shows us that finding area is easy when you understand the techniques and formulas involved. We will look at various shapes, from simple squares to more complex ellipses, and see how to figure out their areas. We even have tools to help, which is great. So, let us get started on figuring out how to find area for different shapes right now.
Table of Contents
- What Exactly is Area?
- Finding Area for Simple Shapes
- Area of Curved and Other Shapes
- Using Online Area Calculators
- Frequently Asked Questions About Area
What Exactly is Area?
Area, in simple terms, is the size of a surface. It is the amount of space that a flat shape occupies. Imagine you have a flat piece of paper. The area of that paper is the total space it covers. My text suggests thinking of area as the amount of paint needed to cover a surface, which is a very helpful way to picture it, actually.
It is the amount of substance or material a figure or object occupies. The area formula defines the space contained within a two-dimensional shape's boundary, its perimeter. Understanding this helps us move on to figuring out the surface areas of three-dimensional objects, too. The perimeter, by the way, helps us calculate the length around the outside of a 2D shape.
Learning how to find area for different shapes gives you a basic geometry skill. This skill is quite useful for many things, like planning projects around your home or even understanding maps. It is a core idea in geometry, so knowing it helps with more advanced topics later. This basic understanding is pretty fundamental, you see.
Finding Area for Simple Shapes
Let us start with some shapes you probably see every day. These are often the first ones people learn about when they want to figure out how to find area. The formulas for these are straightforward and easy to remember, which is good. We will look at rectangles, squares, triangles, and parallelograms. You will find that once you get the hang of these, the others are not so hard, either.
Rectangles
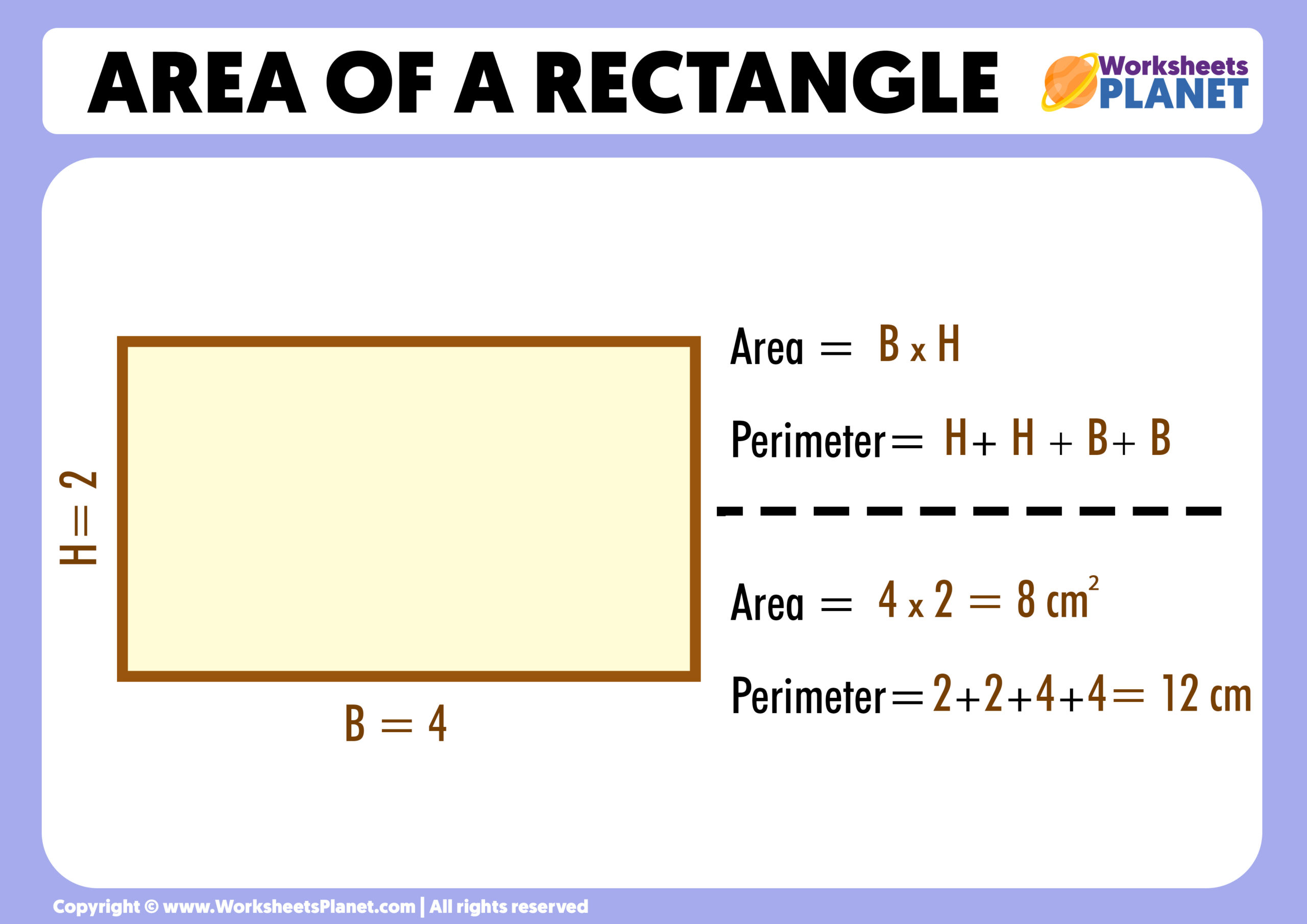
A rectangle is a four-sided shape where all corners are right angles, like the corner of a book. Opposite sides are equal in length. To find the area of a rectangle, you just need two measurements: its length and its width. It is a pretty common shape, so knowing this one is quite helpful, in a way.
The formula for a rectangle's area is: Area = Length × Width. For example, if you have a rectangular garden plot that is 10 feet long and 5 feet wide, you would multiply 10 by 5. That gives you 50 square feet. This means you would need enough soil to cover 50 square feet, which is a good amount, really.
This formula works for any rectangle, no matter how big or small. It is a simple multiplication, so it is quite easy to apply. You can use it for a tabletop, a floor, or even a picture frame. Just get those two measurements, and you are ready to go. It is a fundamental calculation for figuring out space.
Squares
A square is a special kind of rectangle. All four sides of a square are the same length, and all its corners are right angles. Because all sides are equal, finding its area is even simpler than a general rectangle. You only need one measurement, the length of one side, which is convenient.
The formula for a square's area is: Area = Side × Side, or Side squared (Side²). For instance, if a square tile has sides that are 1 foot long, its area is 1 foot × 1 foot, which equals 1 square foot. If the side is 3 meters, the area is 3 meters × 3 meters, making it 9 square meters. That is quite a bit bigger, you see.
Squares are everywhere, from floor tiles to windows. Understanding how to find their area is a very practical skill. It is a quick calculation that can help you with many everyday tasks. So, if you spot a square shape, you now know how to figure out its size.
Triangles
A triangle is a three-sided shape. Finding its area can seem a bit trickier than a rectangle or square, but it is still quite straightforward once you know the formula. You need to know the length of its base and its height. The height is the straight distance from the base up to the highest point, forming a right angle with the base, too.
The formula for a triangle's area is: Area = (1/2) × Base × Height. So, if a triangle has a base of 8 inches and a height of 6 inches, you would calculate (1/2) × 8 × 6. This gives you 4 × 6, which is 24 square inches. My text even has a triangle tutorial with pictures and examples, which is pretty helpful.
Sometimes, you might have the side lengths of a triangle but not the height directly. There are other formulas for those situations, but the base and height method is the most common one. It is a good starting point for any triangle area problem. This formula is quite versatile for many different triangle shapes, honestly.
Parallelograms
A parallelogram is a four-sided shape where opposite sides are parallel and equal in length. Think of it like a rectangle that has been "pushed over" a bit, so its corners are not necessarily right angles. Even though it looks slanted, its area formula is very similar to a rectangle's, which is interesting.
To find the area of a parallelogram, you need its base and its height. The base is one of its sides, and the height is the perpendicular distance between that base and the opposite side. It is not the length of the slanted side, but the straight up-and-down measurement. This distinction is quite important, you know.
The formula for a parallelogram's area is: Area = Base × Height. For example, if a parallelogram has a base of 7 centimeters and a height of 4 centimeters, its area is 7 × 4, which is 28 square centimeters. This formula is quite simple to apply, similar to the rectangle, actually. It is a handy one to remember for these shapes.
Area of Curved and Other Shapes
Not all shapes have straight sides. Circles, for instance, are perfectly round. Then there are shapes like trapezoids, which have one pair of parallel sides, and ellipses, which are like stretched circles. Finding the area for these shapes involves slightly different formulas, but they are still quite manageable, too. Let us look at how to find area for these.
Circles
A circle is a perfectly round shape. To find its area, you need to know its radius. The radius is the distance from the very center of the circle to any point on its edge. It is a key measurement for anything to do with circles, really.
The formula for a circle's area involves a special number called pi (π), which is approximately 3.14159. The formula is: Area = π × radius² (pi times radius squared). So, if a circle has a radius of 5 meters, its area would be π × 5² = π × 25, which is approximately 78.54 square meters. That is quite a bit of space, you know.
Circles are everywhere, from wheels to coins to dinner plates. Knowing how to find their area is very useful for many real-world applications. It is a fundamental formula for round objects. This calculation is a bit different because of pi, but it is still quite straightforward once you get the hang of it.
Sectors
A sector is a part of a circle, like a slice of pizza or a piece of a pie. It is bounded by two radii and the arc connecting them. To find the area of a sector, you need to know the radius of the circle it came from and the angle of the sector at the center of the circle. This is a bit more specific than a full circle, too.
The formula for a sector's area relates to the area of the full circle. It is: Area = (Angle of sector / 360°) × π × radius². For example, if you have a sector with a radius of 10 feet and a central angle of 90 degrees, its area would be (90/360) × π × 10² = (1/4) × π × 100 = 25π, which is about 78.54 square feet. That is a good chunk of the circle, you see.
Sectors appear in various designs and engineering problems. Understanding how to find their area helps with designing curved parts or calculating portions of circular fields. It is a more specialized area calculation, but it builds directly on the circle formula, which is helpful.
Trapezoids (Trapeziums)
A trapezoid, sometimes called a trapezium, is a four-sided shape with at least one pair of parallel sides. These parallel sides are called the bases. The other two sides can be any length and are not necessarily parallel. This shape is a bit more complex than a rectangle or square, but its area is still easy to figure out, actually.
To find the area of a trapezoid, you need the lengths of its two parallel bases (let us call them Base 1 and Base 2) and its height. The height is the perpendicular distance between the two parallel bases. It is the straight vertical distance, not the length of a slanted side. This is a key point, you know.
The formula for a trapezoid's area is: Area = (1/2) × (Base 1 + Base 2) × Height. So, if a trapezoid has bases of 6 inches and 10 inches, and a height of 4 inches, its area would be (1/2) × (6 + 10) × 4 = (1/2) × 16 × 4 = 8 × 4 = 32 square inches. This calculation involves a bit more addition before the multiplication, too.
Trapezoids appear in architecture, land surveying, and design. Knowing how to find their area is practical for many construction or planning tasks. It is a useful formula for shapes that have that specific parallel side arrangement. This shape is often seen in roofs or certain land plots, for example.
Ellipses
An ellipse is like a stretched circle, an oval shape. Think of it as a circle that has been squashed either horizontally or vertically. To find the area of an ellipse, you need to know the lengths of its two radii: the semi-major axis (the longest radius) and the semi-minor axis (the shortest radius). These are measured from the center to the edge along the longest and shortest lines, respectively, too.
The formula for an ellipse's area is: Area = π × semi-major axis × semi-minor axis. For example, if an ellipse has a semi-major axis of 8 feet and a semi-minor axis of 5 feet, its area would be π × 8 × 5 = 40π, which is approximately 125.66 square feet. This is quite a bit of space, you know.
Ellipses are found in planetary orbits, architectural designs, and even in the shapes of certain mirrors or lenses. Understanding how to find their area is useful for more advanced geometry or physics problems. It is a bit like the circle formula, but with two different radii instead of just one, which makes sense, really.
Using Online Area Calculators
My text mentions that you can use online calculators to enter dimensions and get the area instantly. This is a very convenient way to find area, especially if you are not sure about the formula or just want a quick check. These tools can handle many different shapes, which is super helpful. You just pick the shape you need, then put in the numbers.
These online tools often cover a wide range of shapes, including all the ones we have talked about and more. They let you choose from shapes like squares, rectangles, triangles, circles, parallelograms, trapeziums, ellipses, and sectors. Some even offer sixteen or seventeen different shapes, which is a lot, honestly.
Many of these calculators also provide the formulas and explanations alongside the result. This means you can learn as you go, which is a great way to understand how to find area. You can often choose your measurement system, like meters or feet, and input dimensions with separate fields for main units and subunits. This makes them very user-friendly, too.
Using such a tool can save you time and help prevent calculation mistakes. It is a practical resource for students, professionals, or anyone who needs to quickly find an area without doing all the math by hand. They are designed to be intuitive, so they are pretty easy to use for almost anyone. It is a very handy little tool, you see.
Frequently Asked Questions About Area
Here are some common questions people ask when they are trying to figure out how to find area.
What is the difference between area and perimeter?
Area is the amount of space inside a flat shape, like the surface of a table. Perimeter is the total distance around the outside edge of that shape, like the length of trim you would need for the table's edge. My text says the perimeter helps us calculate the length of the boundary of any 2D closed shape, which is a good way to put it, too.
Why is area measured in "squared units"?
Area is measured in "squared units" (like square meters or square feet) because you are multiplying two lengths together. For example, if you multiply a length in meters by a width in meters, the result is in square meters. It represents a two-dimensional space, which makes sense, really.
Can I find the area of irregular shapes?
Yes, you can find the area of irregular shapes, but it is often done by breaking them down into simpler shapes. You can divide an irregular shape into several rectangles, triangles, or other standard shapes, calculate the area of each part, and then add them all together. This approach is quite common for complex figures, you know.
Understanding how to find area for different shapes gives you a basic skill for many everyday tasks. Whether you are figuring out materials for a project or just trying to understand the space around you, these formulas and tools are quite helpful. My text shows that with the right knowledge, finding the area of an object is easy as long as you understand the technique. Learn more about geometric measurements on our site, and link to this page to use our intuitive area calculator tool for instant results. You can also explore more at a reputable geometry resource for additional insights and practice problems. It is a very practical skill, honestly, for so many situations.
How To Calculate The Area Of A House Shape at Phillip John blog

How to Find Area and Perimeter: 11 Steps (with Pictures) - wikiHow

Area Calculator - Calculate Area of Various Shapes